MAGNÉTOHYDRODYNAMIQUE

MAGNÉTOHYDRODYNAMIQUE

La magnétohydrodynamique (M.H.D.) est une branche de la physique consacrée à l’étude des mouvements des fluides conducteurs de l’électricité en présence de champs magnétiques. Elle s’applique aux métaux liquides (mercure, métaux alcalins fondus), aux gaz faiblement ionisés et aux plasmas.

Lorsqu’un fluide conducteur se déplace dans un champ magnétique, il est le siège d’un champ électrique qui y produit des courants électriques; ceux-ci modifient le champ magnétique initial; d’autre part, les forces de Laplace appliquées à la matière le long des lignes de courant modifient le mouvement du fluide. Ainsi apparaît une interaction des effets électromagnétiques et hydrodynamiques qui constitue le domaine d’étude de la M.H.D. L’importance de l’interaction est caractérisée par un nombre sans dimension R^M appelé nombre de Reynolds magnétique; R^M est proportionnel à la conductivité électrique du fluide, à sa vitesse et aux dimensions de l’écoulement. L’interaction est généralement faible (R^M 麗 1) dans les métaux liquides et les gaz faiblement ionisés et forte (R^M 礪 1) dans les plasmas.

Le champ magnétique peut être considéré comme un fluide mélangé au fluide matériel et exerçant sur lui des efforts de «pression magnétique» proportionnels au carré de l’induction magnétique B. Si l’interaction champ-matière est forte, ces deux fluides se déplacent solidairement: le champ magnétique est «gelé» dans la matière. Le milieu peut alors propager des ondes spéciales de basse fréquence appelées ondes magnétohydrodynamiques: les plus simples d’entre elles sont les ondes d’Alfvèn, qui se propagent parallèlement aux lignes de forces magnétiques; ce sont des ondes transversales qui peuvent être considérées comme des oscillations des tubes de force, ceux-ci se comportant comme des cordes vibrantes chargées par la matière entraînée.

La magnétohydrodynamique intervient dans l’interprétation de nombreux phénomènes naturels: champs magnétiques et vitesses de rotation des étoiles et des planètes; taches, éruptions et vent solaires; structure des magnétosphères; origine des rayons cosmiques, rayonnement des pulsars. L’importance de la M.H.D. dans tous ces événements astrophysiques tient au fait que les dimensions, les vitesses et, souvent, les conductivités des plasmas en jeu sont très élevées de sorte que la matière et le champ magnétique sont fortement couplés.

À l’échelle terrestre, de nombreuses applications techniques de la M.H.D. ont été envisagées, certaines dès le XIX^e siècle. Leur développement pratique se heurte à une difficulté importante: les métaux liquides et les gaz ionisés sont, en général, de moins bons conducteurs que le cuivre, de sorte qu’ils ne peuvent se substituer à celui-ci en électrotechnique que dans des cas très spéciaux.

Des développements industriels importants concernent les métaux liquides (pompage électromagnétique du sodium utilisé comme réfrigérant dans certains réacteurs nucléaires; pompage, brassage et lévitation dans certains traitements métallurgiques). Les applications aux gaz ionisés et aux plasmas ont fait l’objet de recherches: confinement magnétique des plasmas dans les recherches sur la fusion contrôlée, conversion d’énergie (générateurs M.H.D. pour améliorer le rendement des centrales thermiques, moteurs M.H.D. pour la propulsion des fusées, souffleries hypersoniques), aérothermie et propulsion navale.

1. Magnétohydrodynamique des liquides

Équations générales de la M.H.D. des liquides

La M.H.D. est consacrée à l’étude des interactions entre le champ de vitesse v et le champ d’induction magnétique B, qui décrivent le mouvement d’un fluide conducteur dans un champ magnétique. Elle est donc régie par un système d’équations couplées obtenu à partir des équations de Maxwell et des équations de l’hydrodynamique. Les premières (cf. ÉLECTRICITÉ - Électromagnétisme) s’écrivent ici sous forme simplifiée:

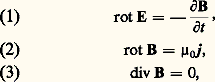où E, B, j sont le champ électrique, l’induction magnétique et la densité de courant. Les simplifications faites sont justifiées par le fait que, d’abord, les liquides considérés ne sont pas magnétiques (B = 猪⁰H); qu’ensuite le courant de polarisation diélectrique et le courant de déplacement de Maxwell sont négligeables devant le courant de conduction j. D’autre part, j est relié aux champs appliqués par la loi d’Ohm relative à un conducteur en mouvement dans un champ magnétique:

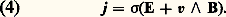Dans cette relation, le champ d’induction v 廬 B s’ajoute au champ électrique E produit dans le repère fixe; la conductivité électrique 靖 est supposée scalaire et non modifiée par la présence du champ B (l’effet Hall est négligeable dans les métaux).

Les équations générales de l’hydrodynamique s’écrivent, d’autre part, également sous forme simplifiée:

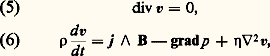où 福, p , 兀 sont la masse spécifique, la pression et la viscosité du fluide. Les équations ainsi écrites sont valables pour un fluide incompressible, visqueux et homogène ( 福 et 兀 constants).

Convexion et diffusion du champ magnétique

En éliminant entre les équations (1) à (4) les variables auxiliaires j et E, on obtient:

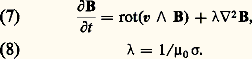L’équation (7) met en évidence le couplage entre le champ B et le champ de vitesse v; si l’on suppose connu v, c’est-à-dire le mouvement du fluide, elle décrit l’évolution de B; c’est ce qu’on peut appeler avec Lundquist l’aspect cinématique de la M.H.D. Les deux termes qui figurent au deuxième membre de l’équation (7) décrivent deux mécanismes différents qui font évoluer B en un point donné: le premier dépend de la vitesse du fluide, le second est proportionnel à sa résistivité. Pour des raisons qui vont être développées, on peut les appeler:

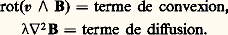Supposons tout d’abord le deuxième terme nul, de sorte que l’équation d’évolution de B se réduit à:

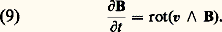Ce cas limite s’obtient en considérant un fluide de conductivité électrique 靖 infinie; pour que j et B restent finis, on doit alors avoir:

Des deux équations (9) et (10) on déduit que le champ magnétique est entraîné par la matière; mathématiquement, cela s’exprime par deux théorèmes de convexion de B représentés sur la figure 1: sur ce schéma, C représente un contour fermé tracé à un certain instant t dans le fluide et MP une ligne confondue à ce même instant avec une ligne de force de B. À un instant ultérieur t , les éléments du fluide se sont déplacés: ceux du contour C tracent un contour C , ceux de la ligne MP décrivent une ligne M P . Les deux théorèmes de convexion de B permettent d’affirmer que le flux du champ magnétique 淋 (C ) à travers C est égal au flux initial 淋 (C) à travers C et que la ligne M P se confond comme MP avec une ligne de force de B.

Ces deux résultats ont été énoncés clairement par l’astrophysicien suédois Hannes Alfvén, en 1942, qui les a résumés en disant que le champ magnétique et la matière constituent deux fluides gelés l’un dans l’autre.

Considérons maintenant le cas limite opposé où le deuxième mécanisme d’évolution de B est dominant, de sorte que l’équation d’évolution de B se réduit à:

Sous cette forme, on reconnaît l’analogue vectorielle de l’équation classique de la diffusion ^{[cf. DIFFUSION DE LA LUMIÈRE (météorologie)]}; est le coefficient de diffusion de B. L’équation (11) exprime le fait que toute perturbation locale de B tend à s’atténuer par diffusion selon le schéma indiqué sur la figure 2. La vitesse de diffusion est d’autant plus faible que la conductivité électrique du fluide est plus grande, parce que les courants de Foucault s’opposent aux variations de B. En un temps de l’ordre de t , la distance de diffusion est de l’ordre de (t )^1/2; la pénétration d’un champ alternatif de pulsation 諸 est limitée à une couche dont l’épaisseur est de l’ordre de (/ 諸)^1/2: c’est l’effet de peau. Remarquons, enfin, que les phénomènes de diffusion décrits précédemment sont indépendants de v qui ne figure plus dans l’équation (11): dans ce cas limite, il n’y a plus aucune convexion de B par la matière.

En pratique, convexion et diffusion se superposent toujours plus ou moins et il est intéressant d’établir un critère caractérisant l’importance relative de ces deux mécanismes. L’analyse dimensionnelle de l’équation (7) le permet; désignons par l une longueur qui caractérise l’échelle de l’écoulement considéré (distance sur laquelle v ou B varie notablement): on voit alors que le terme de convexion est d’ordre vB/l et celui de diffusion d’ordreB/l ². On peut donc former le nombre sans dimension: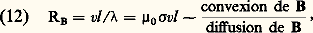

appelé nombre de Reynolds magnétique .

Il y a une importante analogie entre l’équation (7) de transport de B et l’équation qui décrit dans un fluide incompressible, non conducteur, mais visqueux l’évolution de la grandeur 諸 = rot v qu’on peut appeler la vorticité. Celle-ci s’écrit en effet:

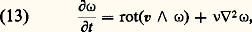où 益 = 兀/ 福 est la viscosité cinématique du fluide. La vorticité se transporte donc également par convexion et par diffusion et le rapport de ces deux effets est caractérisé par le nombre de Reynolds usuel:

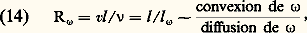avec: l size=1^諸 = 益/v.

Le parallélisme entre les grandeurs relatives à 諸 et B est souligné dans le tableau 1. Pour un fluide donné, on peut former le rapport:

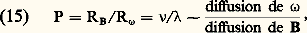appelé nombre de Prandtl magnétique . En pratique pour tous les conducteurs liquides, on a P 廉 1: les champs magnétiques diffusent et s’amortissent beaucoup plus vite que la vorticité.

Tenseur des efforts magnétiques: pression et tension magnétiques

Dans l’équation fondamentale de la dynamique (6), le terme j 廬 B représente la force électromagnétique appliquée à une unité de volume du fluide. En tenant compte de l’équation de Maxwell-Ampère (2), on peut montrer que cette force est la divergence d’un tenseur, c’est-à-dire que l’on a:

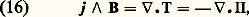où T est le tenseur des efforts magnétiques (tractions) et 刺, son opposé, celui des pressions magnétiques.

En analysant ces tenseurs, on montre que le champ B exerce sur la matière (fig. 3) une pression isotrope, appelée pression magnétique :

et une force de traction dirigée selon les lignes de force (tension magnétique ):

Lorsque le champ B est uniforme, la résultante des forces appliquées à un élément de volume du fluide est nulle (cf. formule 16 et fig. 3). Dans un champ non uniforme, p ^M et ^M varient d’un point à un autre et les lignes de force sont en général courbes. La force résultante j 廬 B n’est plus alors nulle en général; on peut vérifier qu’elle est perpendiculaire à B et l’analyser (fig. 4) en deux composantes: l’une est due au gradient transverse de la pression magnétique; l’autre, dirigée selon le rayon de courbure R de la ligne de force moyenne et égale à B²/ 猪⁰R, est la résultante des forces de traction. On peut vérifier que, lorsque j = 0, la structure du champ est telle (rot B = 0) que ces deux composantes se compensent, de sorte que la force résultante est effectivement nulle.

Ondes d’Alfvén

Lorsqu’un fluide assez conducteur est placé dans un champ magnétique statique B, la propagation des ondes électromagnétiques de basse fréquence s’y fait avec entraînement de la matière par convexion: de telles ondes sont appelées magnétohydrodynamiques (ou parfois hydromagnétiques).

Le cas le plus simple est celui d’ondes planes sinusoïdales se propageant dans un fluide homogène, parallèlement à un champ uniforme B⁰; si la matière et le champ magnétiques sont gelés l’un dans l’autre, on a alors les ondes d’Alfvén transversales dont la structure est représentée sur la figure 5. Elles peuvent être décrites en considérant les tubes de force comme des cordes vibrantes tendues par la tension magnétique ^M et chargées par la matière entraînée par convexion. La vitesse de propagation de ces ondes est alors donnée par la formule classique des cordes vibrantes: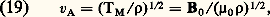

où v^A est la vitesse d’Alfvén ; elle est indépendante de la fréquence. Les ondes d’Alfvén, comme les ondes sonores, sont sans dispersion dans le domaine des basses fréquences. En fait, leur existence suppose une forte interaction champ-matière; le nombre de Reynolds magnétique qui caractérise cette interaction s’écrit ici:

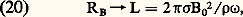où L est appelé nombre de Lundquist.

Pour que les ondes d’Alfvén se propagent sans dispersion ni amortissement notable, il faut que la fréquence soit assez basse et que le champ B⁰ et la conductivité 靖 soient assez forts.

Écoulements de Hartmann

On appelle écoulements de Hartmann une famille d’écoulements stationnaires, laminaires, ayant la structure représentée sur la figure 6: le fluide conducteur, supposé incompressible, s’écoule entre deux plaques parallèles considérées comme infinies. Un champ magnétique uniforme B^z est imposé dans la direction Oz perpendiculaire aux plaques; la vitesse v^y du fluide est dirigée suivant Oy et un champ électrique uniforme E^x peut être appliqué suivant la troisième direction Ox . Les champs électriques E^x et v^y B^z produisent un courant j ^x dirigé suivant Ox ; on dispose le circuit extérieur de façon que les trajets des courants de retour j soient situés dans des plans parallèles à x Oz , et produisent donc avec j ^x un champ induit B^y parallèle à v. Le mouvement est entretenu soit par le champ E^x et la force 漣 j ^x B^z qui en résulte, soit par un gradient de pression 煉p / 煉y . E^x , B^z et 煉p / 煉y sont des constantes, v^y , B^y et j ^x sont des fonctions de z .

Un écoulement de Hartmann possède une vorticité 諸^x dirigée suivant Ox dont l’existence est due au fait que v^y s’annule à la paroi. Sa répartition est le résultat de deux effets contraires: la viscosité qui tend à faire diffuser 諸^x vers l’intérieur du fluide, et le champ magnétique transverse qui s’oppose à cette pénétration. Si B^z est assez fort, la vorticité est confinée au voisinage des parois dans deux couches limites dont l’épaisseur est de l’ordre de:

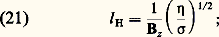l ^H est la longueur de Hartmann, le nombre de Hartmann H étant le rapport a /l ^H où 2 a est la distance entre les plaques. Lorsque H 礪礪 1, la répartition de v^y dans la section droite a l’allure représentée sur la figure 6.

Pompage électromagnétique du sodium dans les réacteurs nucléaires

Parmi les applications des écoulements de Hartmann, seules les pompes électromagnétiques sont dès maintenant entrées dans la pratique industrielle: on les utilise en particulier dans l’industrie nucléaire pour véhiculer le sodium fondu qui est le fluide caloporteur généralement choisi pour les réacteurs surrégénérateurs. Le schéma de principe d’une telle pompe est représenté sur la figure 7.

Les pompes réalisées sont de deux types: pompes à conduction qui dérivent directement du schéma de la figure 7 et où des électrodes relient le fluide à un circuit extérieur; pompes à induction dans lesquelles le fluide est isolé et parcouru par des courants de Foucault induits dans sa masse par un champ magnétique alternatif glissant. La figure 8 indique dans un diagramme débit-pression les domaines d’utilisation des pompes de ces divers types fabriquées en France par la Société G.A.A.A. (Groupement atomique Alsacienne-Atlantique).

2. Magnétohydrodynamique des gaz faiblement ionisés

Équations générales

Un gaz faiblement ionisé est composé essentiellement d’atomes, de molécules neutres et de quelques particules chargées: électrons et ions. Les densités numériques n ⁰, n ^e , n ⁱ de ces trois espèces de particules satisfont aux relations n ^e = n ⁱ (neutralité électrique) et n ^e size=1^廉 n ⁰. Des gaz de ce type se rencontrent en électrotechnique (décharges dans les gaz, convertisseurs d’énergie), en aérodynamique (écoulements hypersoniques) et en géophysique (basse ionosphère).

Les propriétés hydrodynamiques d’un gaz faiblement ionisé sont essentiellement celles du gaz neutre. D’autre part, les forces électromagnétiques appliquées aux particules chargées sont transmises localement aux particules neutres par les collisions électron-neutre et ion-neutre qui sont très fréquentes si la pression n’est pas trop basse. Dans ces conditions, on peut, si l’on se limite à l’étude d’écoulements ne variant pas trop vite dans le temps ou dans l’espace (basses fréquences, grandes longueurs d’ondes), transposer les équations de la M.H.D. aux gaz faiblement ionisés. Cependant, pour tenir compte de la compressibilité du gaz, il faut écrire le système complet des équations hydrodynamiques.

Les équations électromagnétiques de la M.H.D. se transposent sans grandes modifications aux gaz faiblement ionisés. La condition pour que le courant de déplacement soit négligeable s’écrit:

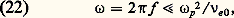ou: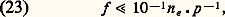

où f , exprimé en hertz, est la fréquence caractéristique de l’écoulement, 諸^p la fréquence de plasma ^{[cf. PLASMAS]} et 益^e0 la fréquence de collision électron-neutre, n ^e étant exprimé en cm^-3 et p en torr. Cette condition étant généralement satisfaite, la seule modification à apporter aux équations électromagnétiques concerne la loi d’Ohm, qui s’écrit maintenant de façon plus générale sous la forme:

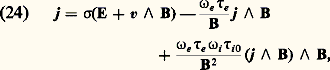où 諸^e et 諸ⁱ sont les fréquences gyromagnétiques des électrons et des ions, 精^e = ( 益^e0 + 益^ei )^-1 la «période de collision» des électrons, 精i ⁰ = 1/ 益ⁱ⁰ la période de collision ion-neutre. Les deux termes supplémentaires qui figurent dans cette formule décrivent deux phénomènes nouveaux qui étaient négligeables dans les liquides: l’effet Hall et le «glissement» des ions par rapport aux neutres. L’importance de ces deux phénomènes est mesurée par les valeurs du paramètre 諸^e 精^e appelé paramètre de Hall et du paramètre correspondant 諸ⁱ 精ⁱ⁰ . La figure 9 donne à titre d’exemple les valeurs de 諸^e 精^e dans un mélange de type argon-césium utilisé dans les convertisseurs d’énergie. On y voit que, pour une pression de 1 atm., l’effet Hall commence à être important ( 諸^e 精^e 黎 1) pour des champs de 0,1 T (1 000 Gs).

Le tableau 2 permet finalement de comparer les propriétés magnétohydrodynamiques d’un gaz faiblement ionisé typique et d’un métal liquide tel que le mercure.

Génération d’électricité par conversion M.H.D.

Bien que les idées de base de la M.H.D. remontent aux travaux de Faraday, c’est surtout depuis 1955 que l’utilisation de gaz ionisés dans des convertisseurs d’énergie a fait l’objet de travaux importants. Le but recherché est la mise au point de générateurs à induction transformant directement l’énergie interne d’un gaz chaud en énergie électrique sans passer par l’intermédiaire de machines tournantes (turbines, alternateurs ou dynamos). Pour cela, on rend le gaz légèrement conducteur de l’électricité en l’ionisant partiellement: l’ionisation est facilitée par l’ensemencement du gaz en atomes alcalins facilement ionisables; elle peut être purement thermique ou augmentée par un champ électrique auxiliaire. Le gaz chaud ionisé est envoyé dans une tuyère M.H.D. qui joue un double rôle: d’une part, le gaz s’y détend et transforme une partie de son énergie thermique en énergie cinétique; d’autre part, la tuyère est le siège d’un champ magnétique transversal B, et le gaz conducteur, qui s’y déplace avec la vitesse macroscopique v, y joue le rôle du rotor d’une dynamo: il est le siège d’un champ électrique induit v 廬 B susceptible de produire un courant dans un circuit extérieur si la tuyère est reliée à celui-ci par des électrodes convenablement placées; le gaz transforme ainsi son énergie cinétique en énergie électrique.

Si le paramètre de Hall 諸^e 精^e est assez faible, le courant j est parallèle à v 廬 B et l’on utilise en général la disposition représentée sur la figure 10 a, dite «générateur de Faraday à électrodes segmentées».

Si le paramètre de Hall 諸^e 精^e est bien supérieur à l’unité, le champ électrique et le courant sont fortement inclinés sur l’axe et l’on utilise alors la disposition de la figure 10 b, dite «générateur de Hall à électrodes segmentées».

Le développement industriel de la conversion M.H.D. d’énergie peut se faire dans différentes voies:

a ) Amélioration du rendement des centrales thermiques à combustibles fossiles par adjonction d’une unité M.H.D. au cycle à vapeur traditionnel (fig. 11). Dans ce cas, les gaz de combustion sont, après traversée de la tuyère M.H.D. et de la chaudière, rejetés dans l’atmosphère: on dit que l’installation fonctionne en cycle ouvert. Le développement de cette technique a fait l’objet d’importantes recherches depuis 1960. On a montré qu’on pourrait ainsi augmenter de 10 p. 100 le rendement des centrales thermiques. Un tel développement doit cependant s’inscrire dans une politique générale de la production d’énergie (prix mondial des combustibles fossiles, «relève» possible des centrales thermiques par les centrales nucléaires).

b ) Centrales nucléaires à conversion M.H.D. L’utilisation de la conversion M.H.D. dans une centrale où la source d’énergie primaire serait la fission nucléaire devrait permettre d’atteindre des rendements très élevés. Dans de telles installations, on pense généralement que le fluide caloporteur serait de l’hélium. Le fluide de travail dans la tuyère M.H.D. serait soit cet hélium, soit de l’argon chauffé dans un échangeur; il est en tout cas ensemencé en atomes alcalins et recyclé («cycle fermé»). Cependant, pour obtenir un rendement suffisant dans la tuyère M.H.D., il faut des températures de gaz de l’ordre de 2 000 ⁰C que ne permet pas à l’heure actuelle la technologie nucléaire. Il est probable cependant que les progrès des réacteurs iront dans le sens de la production de températures plus élevées, peut-être même de cœurs nucléaires gazeux à plus de 3 000 ⁰C, et la conversion M.H.D. aura alors un très grand intérêt.

c ) Générateurs à moteur de fusée. En utilisant comme source de gaz chaud un moteur de fusée, on peut construire des générateurs électriques M.H.D. donnant de grandes puissances pendant des temps assez courts (générateurs de pointe dans les centrales électriques, alimentation de dispositifs spéciaux tels que des souffleries). La figure 12 précise le domaine d’application de tels générateurs.

3. Magnétohydrodynamique des gaz totalement ionisés

Dans un gaz faiblement ionisé, les électrons et les ions sont localement couplés au gaz de particules neutres par les collisions, de sorte que le mélange de ces trois espèces de particules se comporte du point de vue hydrodynamique comme un fluide pur dont la vitesse v est essentiellement celle des particules neutres. Dans un gaz complètement ionisé, celles-ci ont complètement disparu, et on montre de plus ^{[cf. PLASMAS]} que les collisions électron-ion jouent un rôle assez faible dans la dynamique du milieu: il semble donc a priori que l’on doit, en général, pour décrire le mouvement du plasma, utiliser une théorie à deux fluides dans laquelle les densités, vitesses et pressions partielles des électrons et des ions évoluent séparément.

Considérons, cependant, un plasma placé dans un champ magnétique assez fort; les collisions sont négligeables si l’on a:

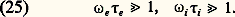Dans ces conditions, si le champ B est à variations spatiales et temporelles suffisamment lentes, les trajectoires individuelles des particules sont en première approximation des hélices dirigées suivant les lignes de force magnétiques. Si, maintenant, on superpose au champ B un faible champ E, on montre ^{[cf. PLASMAS]} que ces hélices dérivent lentement dans la direction perpendiculaire à B; il en résulte que les deux espèces de particules sont animées de la même vitesse macroscopique, dite vitesse de dérive:

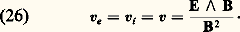Autrement dit, le champ B lui-même introduit un synchronisme entre les deux espèces de particules; on peut donc traiter le plasma comme un fluide unique.

D’autre part, la relation 27 peut aussi s’écrire:

qui est la forme limite que prend la loi d’Ohm (4) lorsque la conductivité électrique 靖 tend vers l’infini.

On peut enfin montrer que le courant de déplacement est négligeable devant le courant de conduction si l’on a:

ce qu’on peut aussi écrire en cm^-3 gauss^-2: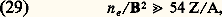

où Ze et A sont la charge électrique et la masse atomique des ions du plasma.

En résumé, si le champ magnétique est assez fort, donc si la condition (25) est remplie, si la fréquence des perturbations est assez basse ( 諸 廉 諸ⁱ ) et le plasma assez dense, donc si la condition (29) est remplie, alors ce plasma se comporte comme un fluide unique satisfaisant aux approximations de la M.H.D. La forme que prend la loi d’Ohm montre de plus que le nombre de Reynolds magnétique est très élevé et que, par conséquent, la convexion de B par le plasma l’emporte sur la diffusion. C’est cette dernière propriété qui détermine les très nombreuses applications des idées de la M.H.D. en géophysique ^{[cf. MAGNÉTOSPHÈRES]}, en astrophysique (cf. ÉTOILES, PULSARS, SOLEIL) et dans les plasmas de laboratoires ^{[cf. PLASMAS]}.

magnétohydrodynamique [ maɲetoidrodinamik ] n. f.

• 1964; de magnéto- et hydrodynamique

♦ Phys. Étude scientifique des fluides conducteurs en mouvement sous l'influence de champs magnétiques ou électriques.

● magnétohydrodynamique adjectif et nom féminin Se dit de la branche de la physique qui étudie l'écoulement des fluides conducteurs en présence de champs magnétiques. (M.H.D. ● magnétohydrodynamique (expressions) adjectif et nom féminin Convertisseur magnétohydrodynamique, ou convertisseur M.H.D., convertisseur d'énergie qui transforme l'enthalpie d'un fluide en énergie électrique ou inversement. ● magnétohydrodynamique (synonymes) adjectif et nom féminin Se dit de la branche de la physique qui étudie...

Synonymes :

- magnétodynamique des fluides

magnétohydrodynamique [maɲetoidʀodinamik] n. f. et adj.

ÉTYM. Mil. XX^e; de magnéto-, et hydrodynamique.

❖

♦ Didact. (phys.). Étude scientifique des charges électrisées en mouvement sous l'influence de champs magnétiques ou électriques. ⇒ Plasma. || La magnétohydrodynamique a permis le confinement de plasmas en vue d'obtenir des réactions de fusion nucléaire.

♦ Adj. || « Machines magnétohydrodynamiques » (la Recherche, oct. 1981).

Encyclopédie Universelle. 2012.